题目/答案
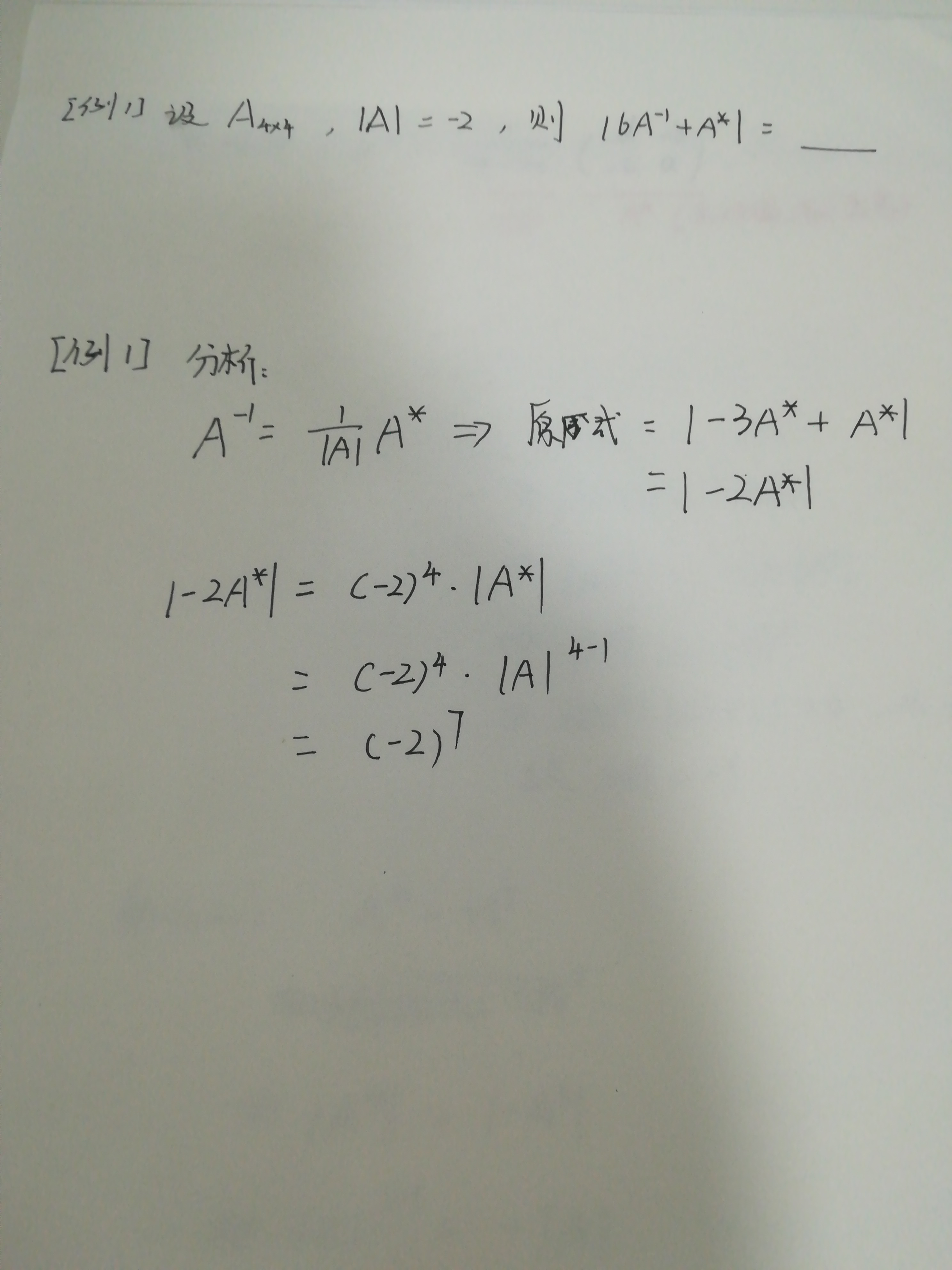
分析
该题类型为利用矩阵公式及定义和所给条件,去计算题目要求的行列式。 一般从化简所求行列式开始入手:化简时,尽量把“A同类化”(如都变成 A^-1或A*或A等),这里可以利用A^-1 = A*/|A|,将式子化成全部由A*组成, 再利用一些性质即可解出。
- 利用公式将A^-1化成A*
- 行列式性质,将系数k提出行列式外,需要将k乘n次方
- 公式:|A*| = |A|^(n-1)
- 合并、带入即可
涉及公式与性质
- A^-1 = A* / |A|
- |kA| = k^n * |A|
- |A*| = |A|^(n-1)